View in other NatureServe Network Field Guides
NatureServe
Montana
Utah
Wyoming
Idaho
Wisconsin
British Columbia
South Carolina
Yukon
California
New York
Toothless Column - Columella edentula
Other Names:
Pupa edentula, Pupa simplex, Vertigo simplex, Columella simplex
General Description
A small shell, about 1.4 mm diameter and 2.5 mm in height, subcylindrical (pupiform) and tapering, with low axial striae, about 5 or 6 whorls, the last larger than the penultimate. Shell coloration is translucent brown to reddish-brown and glossy. Aperture is ovate, unthickened, and without teeth (denticles); periphery rounded; umbilicus is very small (Hendricks 2012, Burke 2013). Internal anatomy is described by Pokryszko (1990).
Diagnostic Characteristics
Columella differs from all other mature shells of similar size and shape by lacking teeth in the aperture, absence of an external crest behind the aperture, and aperture round with a thin lip. C. columella differs from C. edentula by being distinctly more cylindrical instead of clearly tapering to the apex, with 6-7 whorls instead of 5-6, the penultimate whorl before the aperture slightly pinched (smaller) than adjacent whorls instead of with last whorl larger than preceding whorl, height to about 3.0 mm instead of 2.7 mm. Small juveniles resemble Punctum, and can be confused with toothless juvenile Vertigo.
Species Range
Montana Range
Range Descriptions
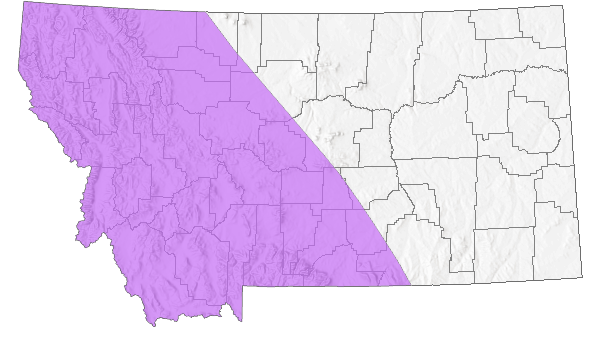
Native
Range Comments
Native from northwest Europe to central Asia and northern North America. In Montana, reported on both sides of the Continental Divide from nine counties: Beaverhead, Broadwater, Cascade, Chouteau, Flathead, Gallatin, Mineral, Ravalli, Sanders. Elevation range is 954 to 2219 m (3130 to 7280 ft). Columella alticola reported by Vanatta from Ravalli County were placed under this species by Henderson. Appears to be uncommon at most locations; up to five were reported at one Beaverhead County site in early July (Hendricks 2012).
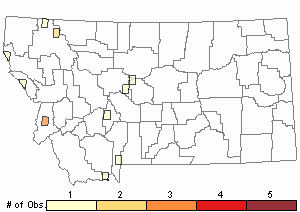
Observations in Montana Natural Heritage Program Database
Number of Observations: 13
(Click on the following maps and charts to see full sized version)
Map Help and Descriptions
Relative Density
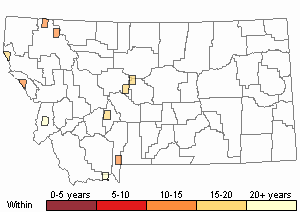
Recency
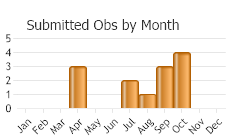
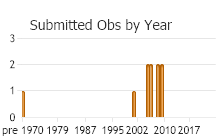
(Observations spanning multiple months or years are excluded from time charts)
Habitat
A diversity of moist sites, including isolated aspen stands. Canopy species include western redcedar, western hemlock, grand fir, Engelmann spruce, Douglas-fir, lodgepole pine, black cottonwood, aspen, paper birch; secondary canopy includes alder, dogwood and mountain maple. Often found under woody debris, on logs and vegetation, and in leaf litter (Hendricks 2012).
References
- Literature Cited AboveLegend:
View Online Publication
Burke, T. E. 2013. Land snails and slugs of the Pacific Northwest. Corvallis, OR: Oregon State University Press. 344 p.- Hendricks, P. 2012. A Guide to the Land Snails and Slugs of Montana. A report to the U.S. Forest Service - Region 1. Montana Natural Heritage Program, Helena, MT. vii + 187 pp. plus appendices.
- Pokryszko, B.M. 1990. The Vertiginidae of Poland (Gastropoda: Pulmonata: Pupilloidae) – a systematic monograph. Polska Akademia Nauk Instytut Zoologii, Annales Zoologici 43:133-257.
- Additional ReferencesLegend: View Online Publication
Do you know of a citation we're missing?- Beetle, D.E. 1989. Checklist of recent Mollusca of Wyoming, U.S.A. The Great Basin Naturalist 49(4):637-645.
- Forsyth, R.G. 2004. Land snails of British Columbia. Royal British Columbia Museum: Victoria, British Columbia, Canada. 188 pp.
- Frest, T.J. and E.J. Johannes. 2001. An annotated checklist of Idaho land and freshwater mollusks. Journal of the Idaho Academy of Science 36(2):1-51.
- Henderson, J. 1924. Mollusca of Colorado, Utah, Montana, Idaho, and Wyoming. University of Colorado Studies 13(2):65-223.
- Pilsbry, H.A. 1948. Land Mollusca of North America (north of Mexico), Volume II Part 2. The Academy of Natural Sciences of Philadelphia Monograph Number 2(2): 521-1113.
- Russell, R.H. and R.B. Brunson. 1967. A check-list of molluscs of Glacier National Park, Montana. Sterkiana 26:1-5.
- Vanatta, E.G. 1914. Montana shells. Proceedings of the Academy of Natural Sciences of Philadelphia 66:367-371.
- Web Search Engines for Articles on "Toothless Column"
- Additional Sources of Information Related to "Snails / Slugs"
